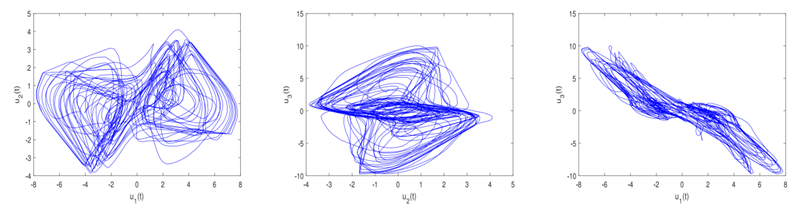
图1 时滞神经网络的混沌动力学
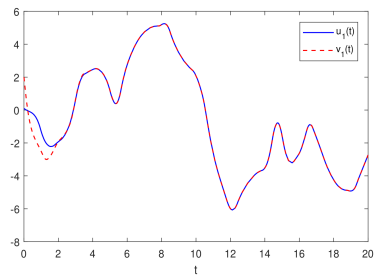
图2 主系统与从系统的状态分量演化
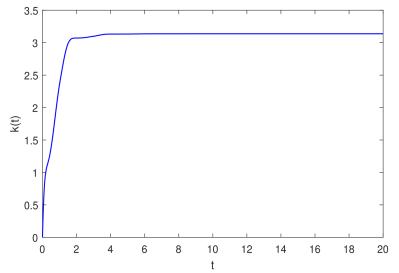
图3 自适应增益的演化
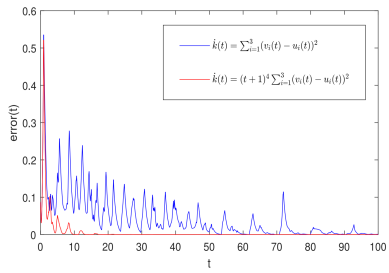
图4 不同自适应律下误差函数的演化
(图文|辛西 编辑|信息 审核|张浩)近日,太阳集团成类脑计算与具身智能团队张浩副教授研究成果“Master–Slave Synchronization of Neural Networks With Unbounded Delays via Adaptive Method”在线发表于人工智能领域国际著名学术期刊IEEE Transactions on Cybernetics上。该工作主要解决了无界不可微时滞神经网络的自适应同步控制问题,揭示了一般时滞对神经网络自适应同步的影响。
同步作为神经网络的一种重要动力学行为反映了外部刺激对网络模型的调节机制,可同步的混沌神经网络可以用于传输和接收加密信号,进而实现信号的安全通信。时滞神经网络的自适应控制问题是神经网络控制中的基本问题之一。该问题的主要分析方法是L-K泛函法,该方法依赖于系统时滞的可微性与有界性,这导致现有的自适应同步设计与分析方法仅适用于具有有界时滞或可微时滞的神经网络模型,而无法解决不可微时滞甚至是无界时滞的自适应同步问题。
针对这一问题,该研究首先建立了一种新的分析方法来分析具有一般时滞的自适应受控系统的收敛性,该方法核心思想是对自适应变化的参数分类讨论,采用Barbalat引理及无界时滞系统稳定性的相关结论,从理论上严格证明了如下结论:即使神经网络中的时滞是不可微分的,甚至是无界的,传统的集中式自适应同步算法对该网络的同步仍然是有效的。不同之处在于,如果时滞是无界的,那么自适应增益的收敛性在这种设计下是得不到保证的,数值例子也佐证了这一观点。
此前研究结果中,自适应算法只能获得渐近收敛的结果,无法获得对误差的收敛性的估计。在无界时滞神经网络的稳定性分析中,有一个重要结论,即随着时滞的变化,误差的收敛速率会由指数向幂数甚至对数收敛转变。鉴于此,该研究提出了一种新的自适应算法,该算法依赖于一类特殊函数,从理论上证明了同步误差可以被该特殊函数所界定,从而获得对误差函数的估计并确保了其渐近收敛性。数值实验的结果表明,该特殊函数的引入能够加速网络同步收敛,但同时也可破坏原有增益的收敛性,而这一点在有界时滞情形是不会发生的。
太阳集团成人工智能系副教授张浩博士为该论文第一作者,华中科技大学人工智能与自动化学院曾志刚教授(IEEE Fellow)为该论文通讯作者。
英文摘要:Master–slave synchronization of two delayed neural networks with adaptive controller has been studied in recent years; however, the existing delays in network models are bounded or unbounded with some derivative constraints. For more general delay without these restrictions, how to design proper adaptive controller and prove rigorously the convergence of error system is still a challenging problem. This article gives a positive answer for this problem. By means of the stability result of unbounded delayed system and some analytical techniques, we prove that the traditional centralized adaptive algorithms can achieve global asymptotical synchronization even if the network delays are unbounded without any derivative constraints. To describe the convergence speed of the synchronization error, adaptive designs depending on a flexible ω-type function are also provided to control the synchronization error, which can lead exponential synchronization, polynomial synchronization, and logarithmically synchronization. Numerical examples on delayed neural networks and chaotic Ikeda-like oscillator are presented to verify the adaptive designs, and we find that in the case of unbounded delay, the intervention of ω-type function can promote the realization of synchronization but may destroy the convergence of control gain, and this however will not happen in the case of bounded delay.
